Вибрации ствола в момент выстрела. Записки технаря
Мудрость индийского йога
От чего зависит кучность — одна из главных характеристик оружия? Очевидно, от качества ствола и патрона. Патрон пока отложим, а рассмотрим физику процесса.
Возьмем металлический стержень или трубочку из упругого металла и жестко закрепим его в массивном основании. Так мы получим модель изучаемого устройства. Теперь, если ударить по стержню, не важно, в каком месте и в каком направлении или оттянуть, или сжать его, или, наконец, вставив в трубочку патрон, произвести выстрел, мы увидим, что стержень (ствол) пришел в затухающее колебательное движение. Эти колебания раскладываются на простейшие, и каждый вид такого простейшего колебания ствола будет влиять на кучность (точность) стрельбы по-своему.
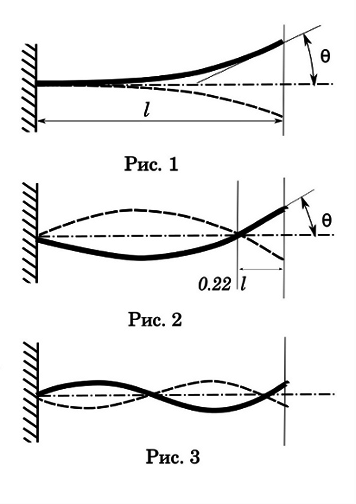
Начнем с колебаний первого порядка или основного тона. Как видно (рис. 1), у такого колебания всего один узел в точке крепления, самая большая амплитуда, самое большое время затухания и самое длительное время колебания одного периода. Это время составляет 0,017-0,033 сек. Время прохождения пули по каналу ствола составляет 0,001-0,002 сек. То есть значительно меньше цикла одного колебания, а значит и существенного влияния на кучность одиночного выстрела такой вид колебаний не оказывает. А вот при автоматической стрельбе может получиться интересная картина. Допустим, темп стрельбы 1200 выст/мин, т.е. время одного цикла - 0,05 сек. При периоде колебаний первого порядка 0,025 сек имеем кратное соотношение частот. А это непременное условие резонанса со всеми вытекающими из этого последствиями — оружие начинает трясти с такой силой, что оно может развалиться.
Перейдем к колебаниям второго порядка (рис. 2). Но гуманитариям предлагаю прежде провести эксперимент, чтобы ликвидировать недостатки образования из области физики. Нужно взять маленького мальчика (можно девочку), посадить на качели и раскачать. Перед вами маятник. Встаньте сбоку от качелей и попробуйте попасть в мальчика мячиком. После ряда попыток, вы придете к заключению, что попасть лучше всего можно тогда, когда цель находится в первой фазе колебания — максимального отклонения от точки равновесия. В этой точке цель имеет нулевую скорость.
Посмотрим на схему второго порядка. Второй узел колебаний находится примерно на расстоянии 0,22 от конца ствола. Эта точка - закон природы, невозможно создать такие колебания для консольной балки, чтобы второй узел приходился на свободный конец. Он там где есть и от длины ствола не зависит.
Амплитуда колебаний у схемы второго порядка ниже, а вот время колебания уже сравнимо со временем прохождения пули по каналу ствола — 0,0025-0,005 сек. Так что для одиночной стрельбы это уже представляет интерес. Чтобы было понятно, о чем речь, представим себе ствол длиной 1 метр. Пуля проходит весь ствол за 0,001 сек. Если период колебания 0,004 сек, то к моменту вылета пули, ствол достигнет максимального изгиба в первой фазе. Вопрос гуманитариям - в какой момент (в какой фазе) лучше всего вылетать пуле из ствола, чтобы обеспечить постоянство результатов? Вспомните качели. В нулевой точке вектор скорости отклонения ствола максимален. Пуле попасть в эту точку на срезе ствола труднее, она же имеет свою погрешность в скорости. То есть, наилучшим моментом вылета пули будет когда ствол находится в самой верхней точке первой фазы отклонения - как на рисунке. Тогда незначительные отклонения в скорости пули будут компенсироваться бОльшим временем нахождения ствола в его наиболее стабильной фазе.
Графическое представление этого явления хорошо видно на схеме (рис. 4-5). Здесь - Δt погрешность по времени, с которым пуля пересекает дульный срез ствола. На рис. 4 идеальный вариант когда среднее время вылета пули совпадает с нулевой фазой колебания ствола. (Математики! Я знаю, что распределение скоростей нелинейно.) Затененная область - это угол разброса траекторий.
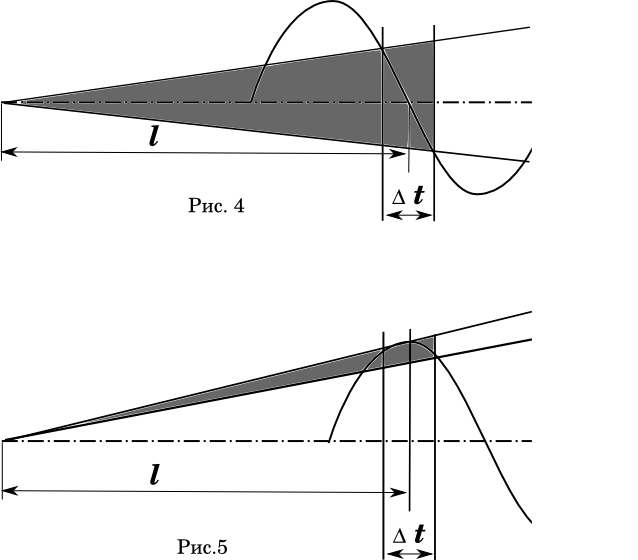
На рис.5 длина ствола и погрешность скоростей остались прежними. Но фаза изгиба ствола сдвинута так, что среднее время вылета совпадает с максимумом отклонения ствола. Комментарии излишни?
Ну, а стоит ли овчинка выделки? Насколько серьезными могут быть отклонения вызванные колебаниями второго порядка? Серьезны и даже очень. По данным советского профессора Дмитрия Александровича Вентцеля, в одном из экспериментов получены следующие результаты: радиус срединного отклонения вырос на 40% при изменении длины ствола всего лишь на 100 мм . Для сравнения — качественная обработка ствола может улучшить кучность всего лишь на 20%!
Теперь взглянем на формулу частоты колебаний:
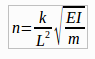
где:
k — коэффициент для колебаний второго порядка — 4,7;
L — длина ствола;
E — модуль упругости;
I — момент инерции сечения;
m — масса ствола.
… и приступим к анализу и выводам.
Очевидный вывод из рисунков 4-5 - это скоростная погрешность пули. Зависит она от качества пороха и его навески и плотности в патроне. Если эта погрешность будет составлять хотя бы четверть времени цикла, то на всё остальное можно махнуть рукой. К счастью, наука и промышленность добились очень большой стабильности в этом вопросе. А для особо искушенных (в бенчресте, например) есть все условия для самостоятельной сборки патронов, чтобы точно под длину ствола подогнать фазу вылета пули.
Итак, у нас есть патрон с минимально возможным разбросом скоростей. Длину ствола раcсчитали, исходя из его предельной массы. Возникает вопрос стабильности. Смотрим на формулу. Какие переменные влияют на изменение частоты колебаний? Длина ствола, модуль упругости и масса. Во время стрельбы ствол нагревается. Может ли нагрев изменить длину ствола, так чтобы это сказалось на точности. И да, и нет. Да, так как эта цифра лежит в пределах сотых долей процента для температуры 200 С. Нет, так как изменение модуля упругости стали для той же температуры примерно 8-9%, для 600С — почти в два раза . То есть многократно выше! Ствол становится мягче, фаза изгиба ствола сдвигается вперед к моменту вылета пули, кучность падает. Ну, что скажет вдумчивый аналитик? Он скажет, что невозможно получить на одной длине ствола максимальную кучность на холодном и горячем режиме! Оружие может иметь лучший показатель или с холодным или с горячим стволом. Соответственно, получается два класса оружия. Одно для засадных действий, когда цель необходимо поразить с первого - «холодного» выстрела, потому что кучность второго будет хуже из-за неминуемого разогрева ствола. В таком оружии нет острой необходимости в автоматике. И второй класс — автоматические винтовки, длина ствола которых подогнана под горячий ствол. В этом случае возможный промах из-за низкой кучности холодного выстрела можно компенсировать быстрым последующим горячим и более точным выстрелом.
Физику этого процесса прекрасно знал Е.Ф.Драгунов, когда проектировал свою винтовку. Предлагаю ознакомиться с рассказом его сына Алексея. Но для начала кое-кому придется сломать мозг. Как известно, к финалу конкурса на снайперскую винтовку подошли два образца Константинова и Драгунова. Конструкторы были друзьями и во всем помогали друг другу. Так вот, винтовка Константинова была «настроена» на холодный режим, винтовка Драгунова на «горячий». Пытаясь улучшить показатель кучности винтовки «соперника», Драгунов ведет стрельбу из его винтовки с длительными паузами.
Посмотрим еще раз на формулу. Как видно, частота зависит и от массы ствола. Масса ствола величина постоянная. Но жесткий контакт с цевьем образует непредсказуемую положительную обратную связь на ствол. Система — ствол-цевье-рука (опора) будет иметь другой момент инерции (совокупность масс относительно точки крепления), а значит и это тоже может вызвать сдвиг по фазе. Вот почему спортсмены используют мягкую опору. С этой же особенностью связано применение принципа «вывешенного ствола», когда цевье оружия не имеет жесткого касания со стволом и жестко крепится к нему (оружию) только в районе ствольной коробки, а второй конец или вообще не касается ствола или касается через подпружиненное сочленение (СВД).
Заключительная мысль. То, что при одной длине ствола невозможно получить одинаковую кучность на разных температурах, дает прекрасный повод поразмять мозги. Нужно всего лишь при изменении температуры ствола изменить его длину и (или) массу. Не изменяя при этом ни длину, ни массу ствола. С точки гуманитария это парадокс. С точки зрения технаря, идеально поставленная задача. С решением таких задач связана вся жизнь конструктора. Шерлоки отдыхают.
Литература:
Благонравов А.А. Основы проектирования автоматического оружия

Информация