Акустический след беспилотников. Возможности обнаружения, идентификации и противодействия

Украинская система акустического наблюдения
Я занимаюсь разработкой прикладной математики и программ для обработки акустических сигналов в системах связи. Моя первая статья на «Военном Обозрении» по акустике беспилотников была несколько простой, не вызвала особого большого изначального интереса, но потом она была единственной из моих статей, которую постоянно кто-то читал. Поэтому я счел необходимым еще раз вернуться к теме с учетом замечаний в комментариях.
На этот раз я скачал существенно более качественные записи украинских беспилотников («Лють» и более мелкие), и рассмотрение можно начать с временной картинки записи с микрофона одного из них.
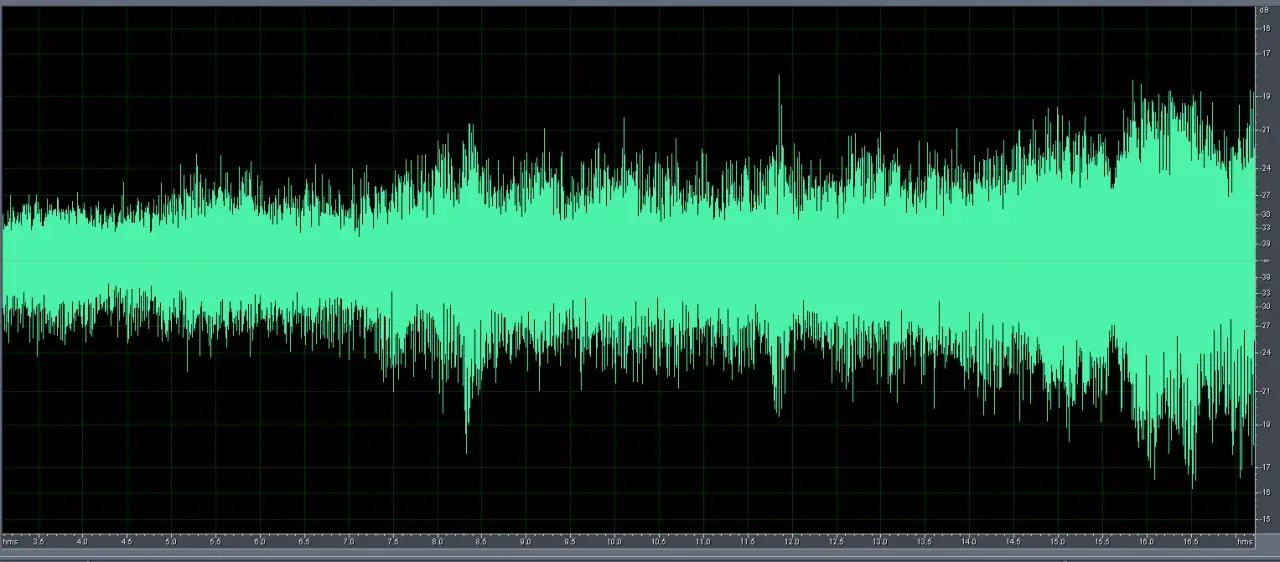
При увеличении временной картинки (осциллограммы) мы уже видим детали, которые вполне можно интерпретировать.
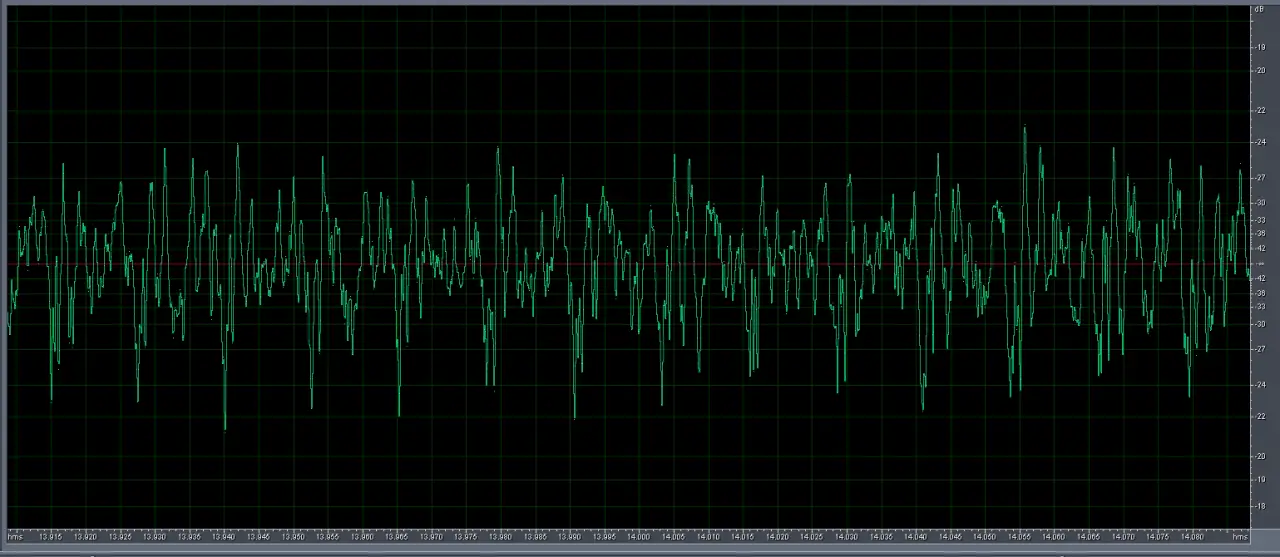
При всем внешнем хаосе здесь мы явственно видим период регулярных тычков, которые являются не чем иным, как тактами выхлопа цилиндров двигателя. Конечно, для анализа замеров в числах тут надо еще разбираться в количестве цилиндров, тактности двигателя, особенности фаз газораспределения по цилиндрам, но эта задача понятная и достаточно прямолинейная.
Данный вид сигнала относится к гармоническому классу. Что это такое. В эволюции наш слух был «заточен» на восприятие трех классов сигналов:
- всплески (в английском это транзиенты), например хруст ветки под ногами;
- шумы, примером которых может быть часть согласных звуков;
- гармонические сигналы, представленные и нашими гласными звуками, звуками животных, пением птиц.
Особенностью гармонических сигналов является то, что они на основном своем участке представляют собой примерно периодический сигнал, который весьма сильно отличается от элементарного синуса. Это создает массу гармоник, кратных основной частоте.
И тот же самый сигнал в частотном представлении будет выглядеть как масса параллельных линий, равноудаленных на величину частоты основного тона.
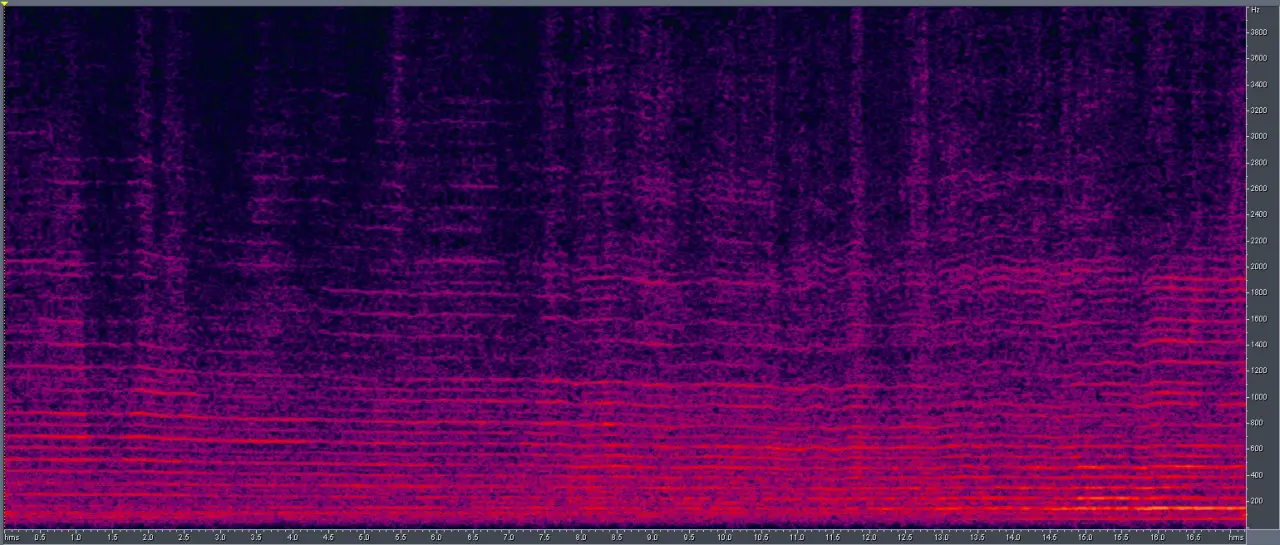
В спектре беспилотника нет особого подчеркивания каких-то частотных зон, как это есть, например, в гласных звуках нашей речи. Основная энергетика лежит в зоне ниже 1,5–2 кГц.
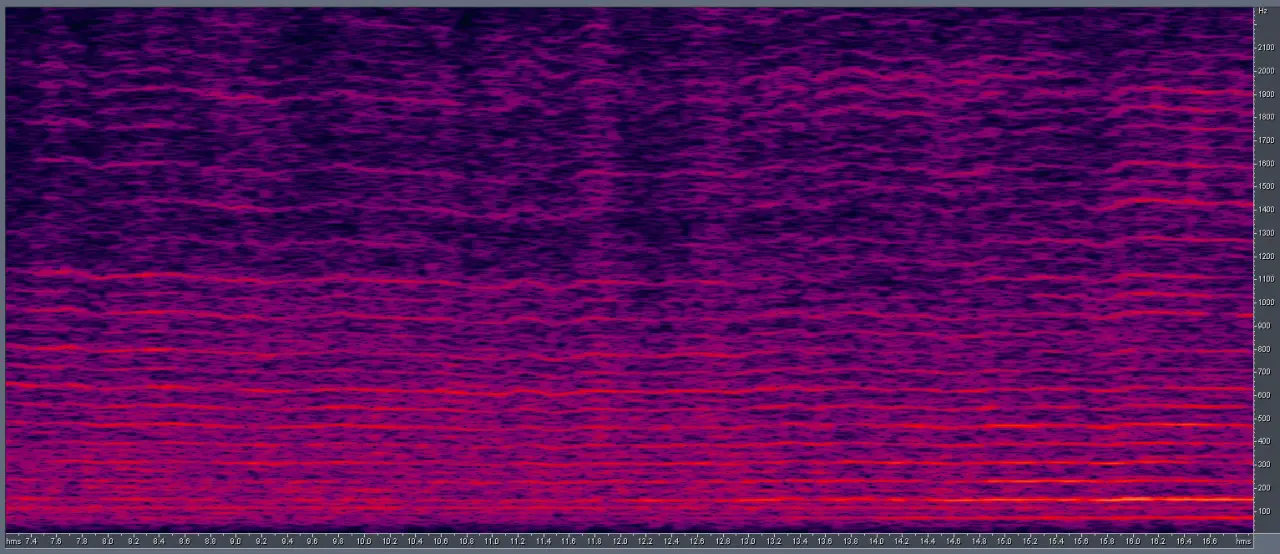
В целом обороты двигателя беспилотника весьма стабильны, хотя просматривается работа регулятора оборотов двигателя. В случае беспилотника нагрузкой двигателя является винт, который обладает какими-то параметрами инерции. Если же мы посмотрим на классические транспортные средства, то там двигатель завязан на колеса, а объектом инерции выступает уже всё транспортное средство вместе с пассажирами. И подобной волнистости в спектральной картинке, очевидно, там мы уже не увидим. Если нужна более точная картина данного явления, то придется погружаться в преобразования Лапласа, классическую теорию управления и горы цифровых данных.

Если мы сделаем срез спектральной картинки в любой временной точке, то спектр будет выглядеть примерно так.
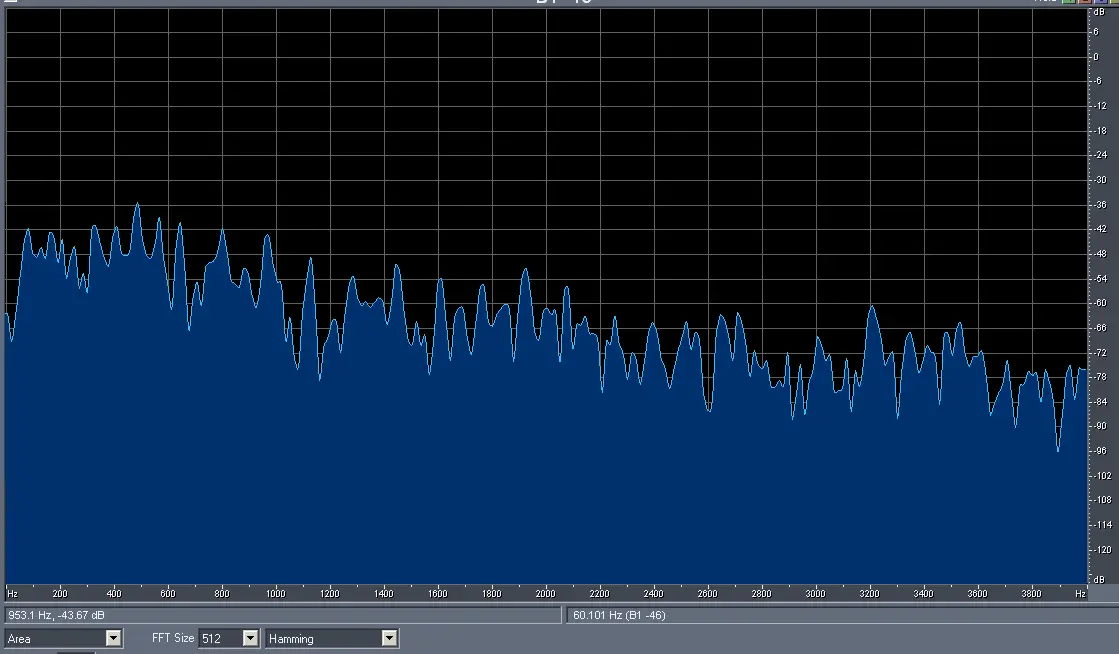
Здесь мы видим амплитуды гармоник (в логарифмическом масштабе) на частотах, кратных основной частоте. Кстати, в биологии есть какой-то закон, согласно которому наше ощущение пропорционально логарифму от величины раздражителя (например, акустического давления). Представленный срез имеет тоже периодический характер.
Технически, он был получен Фурье-преобразованием, крайне полезной математической и вычислительной операцией.
Но здесь любопытно то, что вот эту картинку из-за ее периодичности можно пропустить через Фурье еще раз. Эта операция называется кепстром, и ее меня просили опробовать в комментариях предыдущей статьи.
В этом случае из Фурье «вылезет» период основной частоты пичков (дистанция между гармониками в спектрограмме, но выраженные в обратной форме к частоте — периоде).
Это нам позволяет автоматически прицелиться на данный гармонический сигнал и делать по нему выводы о его принадлежности.
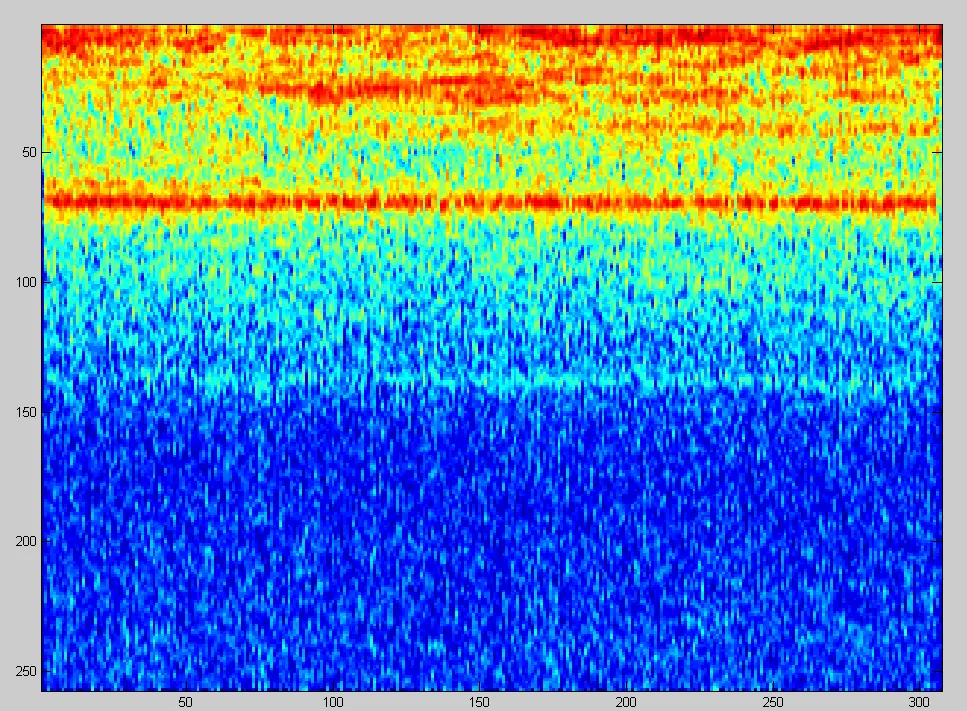
По горизонтали здесь, как и на всех графиках, — время, по вертикали — величина, кратная периоду (но можно говорить и о частоте) основного тона, цвет — интенсивность. Стабильная горизонтальная прямая линия демонстрирует постоянство оборотов двигателя. На кучу всяких артефактов сверху не стоит обращать внимания, поскольку данную программу я писал под совершенно другую исследовательскую задачу.
В другой записи украинского беспилотника явно наблюдается доплеровский эффект в его пролете.
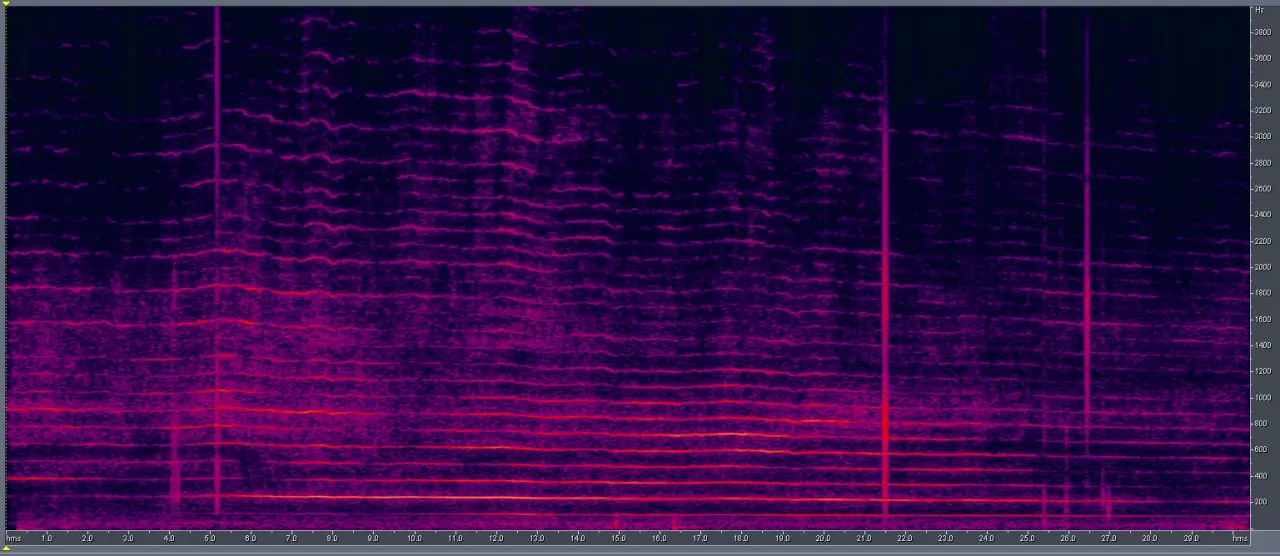
И на кепстре мы видим линейное изменение положения периода основной частоты.
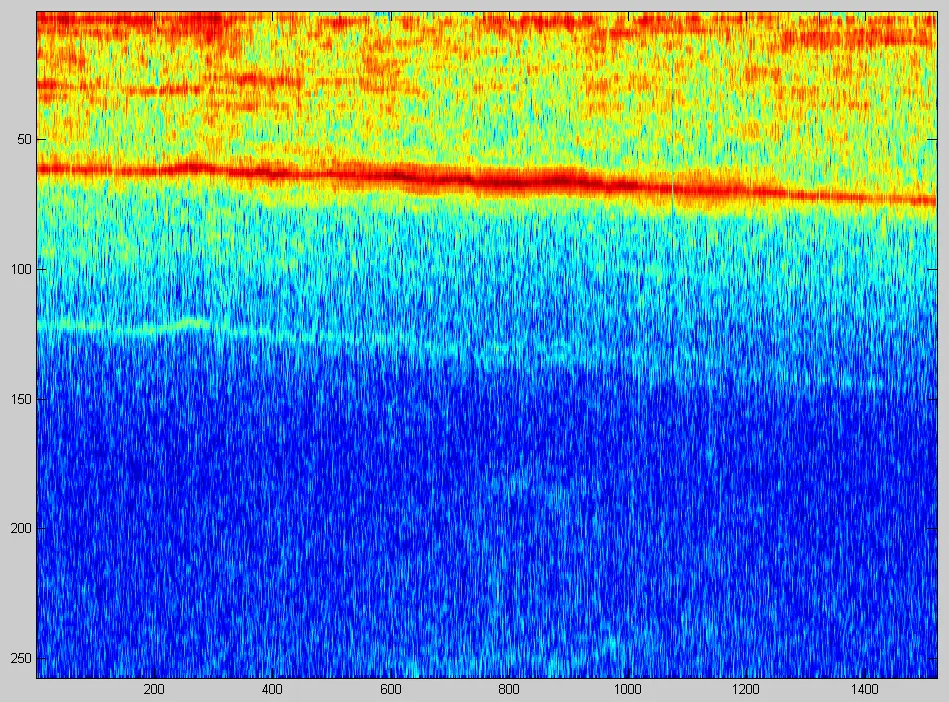
Наш интерес к кепстру вызван тем, что большой поток данных с микрофона по итогу сводится к наблюдению за одной выделяющейся точкой. Это «упаковывает» данные и позволяет существенно снизить скорости передачи по каналу связи. Однако, если мы по кепстру определили частоту основного тона, получили картинку Фурье не с одного, а двух немного разнесенных микрофонов, то на них мы получим практически идентичные картинки амплитуд, но фазы гармоник при этом будут различаться (разница фаз — произведение номера гармоники на величину основной частоты и на величину временной задержки).
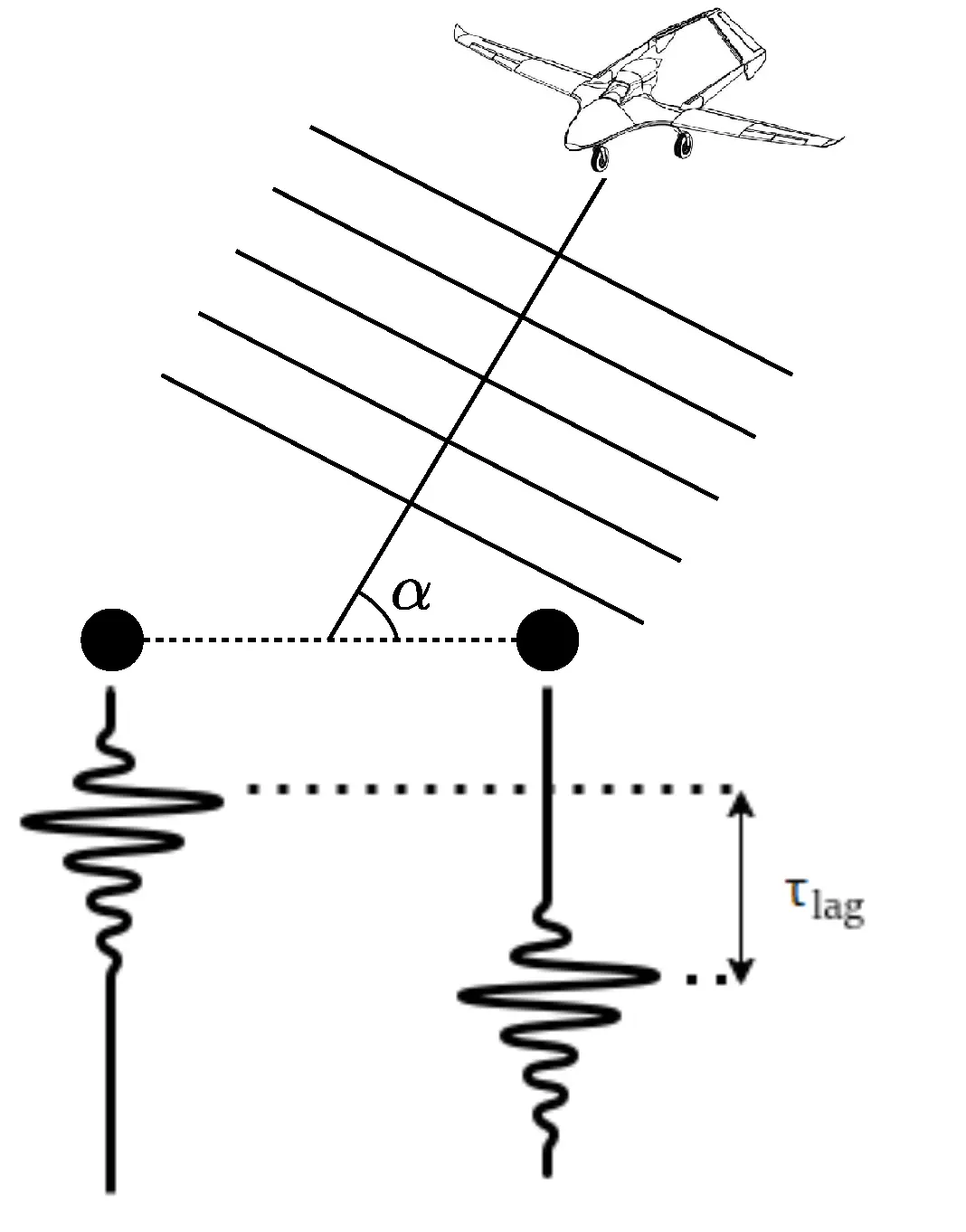
Мы можем принудительно обнулить весь спектр посторонних сигналов, амплитуды гармоник зафиксировать на какой-то постоянной для всех гармоник величине, а в качестве фазы можно засунуть разницу фаз между микрофонами для каждой частоты гармоники.
Если эту комбинацию снова «засунуть» в Фурье (с входом в комплексных числах), то для какого-то выхода Фурье фазы гармоник сложатся в пик (правда, вялый), и это даст нам направление на источник акустического сигнала. Пик этот плоский и не сильно удобный, однако для какого-то другого выхода гармоники будут складываться как «фаза-противофаза», и получится острый минимум, который можно и использовать для определения направления на источник звука.
Я работаю в крупной частной фирме. Здесь иногда на горизонте появляются весьма суровые проблемы, и требуется высокая степень подготовленности к их решению. Одним из моих инициативных исследовательских проектов была работа с условным названием «самонаводящийся микрофон». Все изложенные выше идеи имеют корни из этой работы. Сама же та работа была остановлена по той причине, что я исследую несколько подходов (на практике выживает и доходит до ценного результата только одна идея из 3–5). Те идеи, которые я впитал из лекций МГУ (канал izoalex на «Ютубе»), для наших задач дали существенно более крутые результаты (к слову говоря, эти преподаватели создали математику iZotope RX, мирового лидера в своей области и... американской фирмы).
Во всей этой проблематике выделяются, конечно, коптеры, которые создают максимальные проблемы нашим ребятам.
Спектрограмма звука коптера выглядит так:
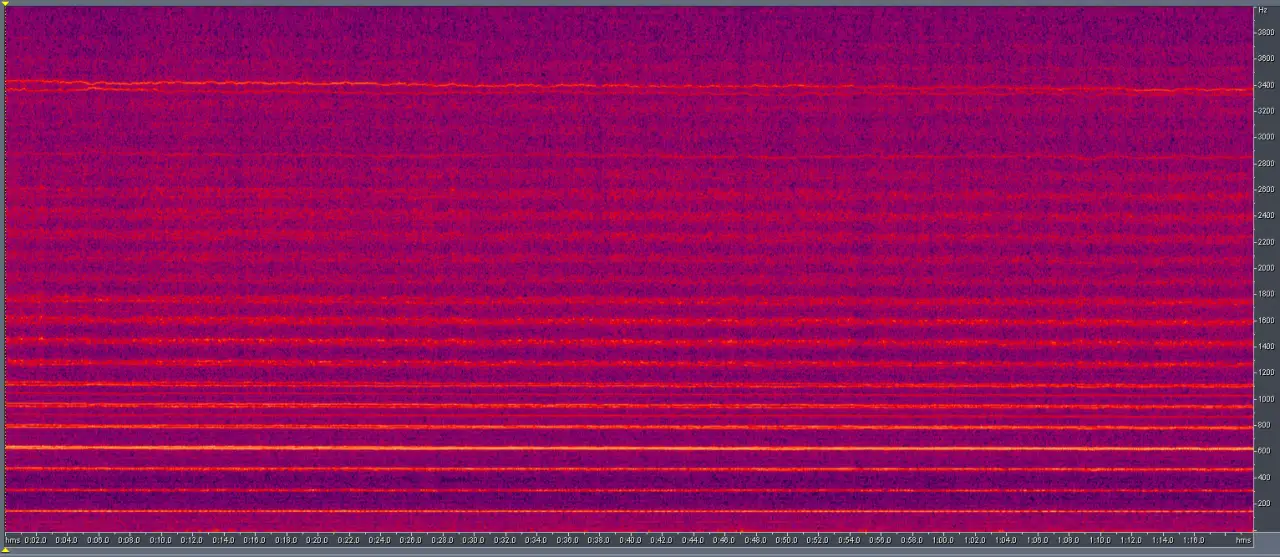
Увеличено в низкочастотной части:
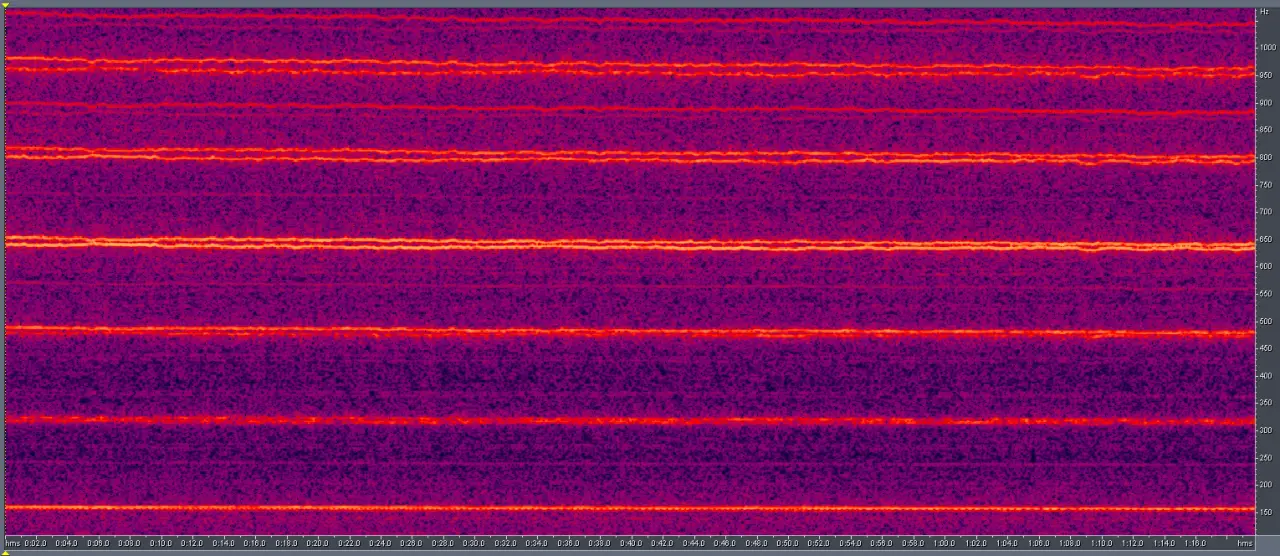
При этом кепстр выглядит как:
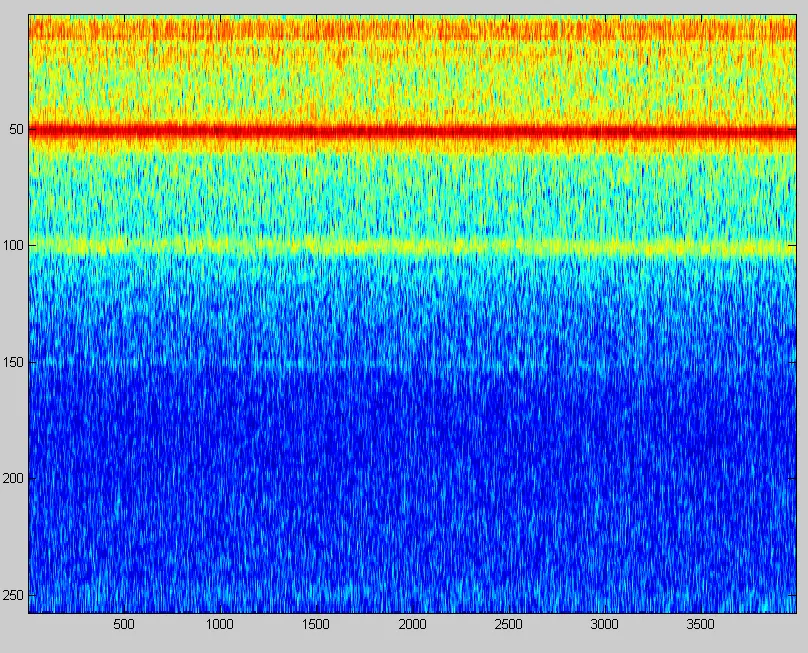
Что их всего этого можно было бы извлечь практически
1. Все эти операции, перечисленные выше в варианте на 4 микрофона (2 микрофона мало из-за снижения углового разрешения в некоторой зоне направлений и отсутствия разделения зеркальных комбинаций), требуют вычислительной мощности, примерно соответствующей микроконтроллерам STM32F4xx или STM32F7xx (это то, что мы можем увидеть в полетных контроллерах коптеров).
Предполагаемая задержка в обработке сигнала будет в районе 30–60 миллисекунд.
2. В области DSP (digital signal processing — цифровая обработка сигналов) у нас в стране работает и обучается не так много людей. Преподавателям в вузах можно было бы дать, к примеру, стерео-записи звука (.wav формата, в котором фаза не удалена из-за компрессии) пролетающего коптера и посмотреть, на что эти преподаватели способны.
Здесь сложности заключаются в том, что теория сигнальной обработки достаточно большая, сложная и опирается на большие объемы разнообразной математики. Вторым осложняющим фактором является то, что профессиональное программирование в этой области крайне далеко от того, чем занимаются обычные программисты.
Отсутствие подобных записей (хотя бы стерео .wav-формата с пары разнесенных микрофонов) меня и остановило в написании продолжения этой статьи.
Информация